ST117 Lab 6

Statistical Estimations

Author

Mengqi Chen, Yujing Lu

Published

February 26, 2024

Statistical Estimations

MLE for Common Distributions

Bernoulli Distribution

\(\hat{p} = \frac{1}{n}\sum_{i=1}^{n}x_i\), where \(x_i\) are the observed values.

Binomial Distribution

\(\hat{p} = \frac{\bar{x}}{n}\), where \(\bar{x}\) is the sample mean.

Poisson Distribution

\(\hat{\theta} = \bar{x}\), where \(\bar{x}\) is the sample mean.

Normal Distribution

\(\hat{\mu} = \bar{x}\) and \(\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2\).

Criteria for Comparing Estimators

  • Bias: \(\operatorname{Bias}(\hat{\theta}) = \mathbb{E}(\hat{\theta})-\theta\)
  • Variance: \(\operatorname{Var}(\hat{\theta})\) Measures the dispersion of the estimator’s distribution.
  • Mean Squared Error (MSE): \(\operatorname{MSE}(\hat{\theta}) = \mathbb{E}(\hat{\theta}-\theta)^2 = \operatorname{Bias}(\hat{\theta})^2 + \operatorname{Var}(\hat{\theta})\) The average squared difference between the estimated values and the actual value. MSE = Bias^2 + Variance.
  • Consistency: An estimator is consistent if it converges in probability to the true parameter value as the sample size increases. For this course, you can check consistency by checking if \(\operatorname{MSE}(\theta)\to 0\) as \(n\to\infty\).

Example: MLE for a Poisson Distribution

We will find the MLE of a Poisson sample, plot the log-likelihood function, find its maximum, and compare with the theoretical value. Recall that the Possion distribution:

\[ P(X=x)=\exp^{-\theta}\frac{\theta^x}{x!} \]

Data Simulation

# Simulating a Poisson-distributed sample
set.seed(123)
theta_true <- 4
n_samples <- 10
sample_data <- rpois(n_samples, theta_true)

sample_data
 [1] 3 6 3 6 7 1 4 7 4 4

Log-Likelihood Function and Plot

The log-likelihood function for Possion distribution:

\[ \begin{align} l(\theta;\vec{x}) &= -n\theta + \ln{\theta}\cdot \left(\sum_{i=1}^n x_i\right) - \underbrace{\ln \left(\prod_{i=1}^n x_i!\right)}_{\text{constant in }\theta} \\ \end{align} \]

log_likelihood <- function(theta, data) {
  sum(data)*log(theta)-length(data)*theta
}

theta_seq <- seq(1, 8, by = 0.1)
ll_values <- sapply(theta_seq, log_likelihood, data = sample_data)

plot(theta_seq, ll_values, type = "l", main = "Log-Likelihood Function", xlab = "theta", ylab = "Log-Likelihood")

MLE <- mean(sample_data)
abline(v = MLE)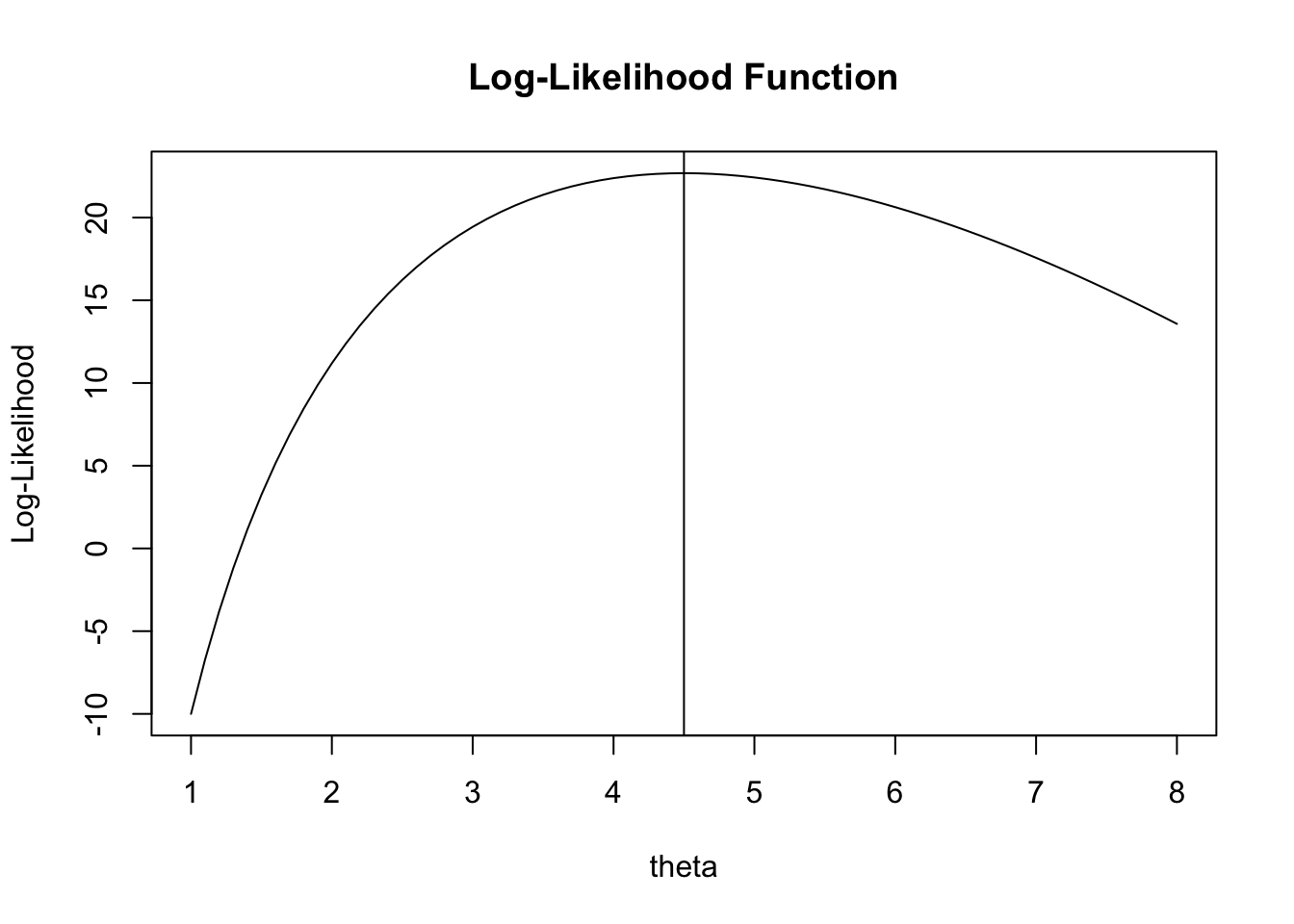

Finding the Maximum

opt1 <-optimize(f=log_likelihood, data = sample_data, interval=c(0,7),maximum=TRUE) 

optimiser <- opt1$maximum

cat("The MLE for theta is:", MLE, "\n")
The MLE for theta is: 4.5 
cat("The optimiser for the log-likelihood is", optimiser, "\n")
The optimiser for the log-likelihood is 4.499999

Assignments

Your turn!
  1. Please attempt these questions and write down your answers in the R Mardown workbook.
  2. Run your codes in your workbook and compare your results with your deskmate.
  3. Knit your workbook to publish a report in PDF or html.

1. Bernoulli Distribution

Suppose we observe data \(\vec{x}=(1,0,0,1,0,1,0,0,1,1)\) where each element \(X_i\) follows a Bernoulli distribution with an unknown success probability \(p\).

  1. Find the likelihood function \(L(p;\vec{x})\) which represents the joint pdf function of \(p\) given the observed data \(\vec{x}\) and define it as a function in R. Calculate the value of this function at \(p=0.1\).

  2. Plot the likelihood function for \(p\in[0,1]\) and use the optimize() function to find the point that maximizes \(L(p;\vec{x})\). Add a vertical line to the plot to indicate this maximum point.

  3. Calculate the log-likelihood function \(l(p;\vec{x})\) and define this function in R. Plot the log-likelihood function. Verify that \(p=0.5\) maximizes the log-likelihood function by setting its first derivative equal to zero and ensuring that the second derivative is negative.

2. Binomial Distribution

Given that \(X \sim \text{Bin}(n,p)\) and observed that \(n=10\) and \(x=3\).

  1. Define the likelihood function in R and calculate it at \(p=0.1\).

  2. Plot the likelihood function for \(p\in[0,1]\) and calculate the maximum likelihood estimate. Add a vertical line to the plot to indicate this maximum point.

3. Normal Distribution

Given the heights(in cm) of a random sample of 20 students:

182, 154, 147, 150, 164, 177, 169, 173, 160, 173, 170, 160, 178, 175, 154, 179, 168, 188, 172, 162

We assume that the heights of students follow a normal distribution with unknown mean \(\mu\) and standard deviation \(\sigma\).

  1. Determine the maximum likelihood estimates of \(\mu\) and \(\sigma\) based on the given sample.

  2. Calculate the log-likelihood of these height estimates.